Python exemplarisch
deutsch     english

Clusteranalyse

 

Alle Programme können von hier heruntergeladen werden.

 

Problembeschreibung
 

Unter Clusteranalyse (Clustering-Algorithmus, gelegentlich auch: Ballungsanalyse) versteht man Verfahren zur Entdeckung von Ähnlichkeitsstrukturen in (großen) Datenbeständen. Die so gefundenen Gruppen von "ähnlichen" Objekten werden als Cluster bezeichnet und die
Gruppenzuordnung als Clustering. Die Clusteranalyse ist eine wichtige Disziplin des Data-Mining-

Diese neuen Gruppen können anschließend beispielsweise zur automatisierten Klassifizierung, zur Erkennung von Mustern in der Bildverarbeitung oder zur Marktsegmentierung eingesetzt werden

Verfahren der Clusteranalyse gewinnen in der Forschungspraxis zunehmend an Bedeutung. Sie werden in zahlreichen Wissenschaftsdisziplinen zur Lösung von Klassifikationsaufgaben eingesetzt. In den Sozial- und Wirtschaftswissenschaften beispielsweise zur Identifizierung von Marktsegmenten. Die Clusteranalyse ist ein algorithmisches Verfahren zur objektiven Klassifikation von Objekten, die durch Merkmale beschrieben werden. Dabei werden ähnliche Objekte in gleiche Klassen eingeteilt.

Das Ziel der Analyse von Daten und deren Zuordnung ist es, dass die Objekte innerhalb eines Clusters möglichst ähnlich (homogen) sind. Die Cluster selbst sollen untereinander möglichst unterschiedlich (heterogen) sein.

 

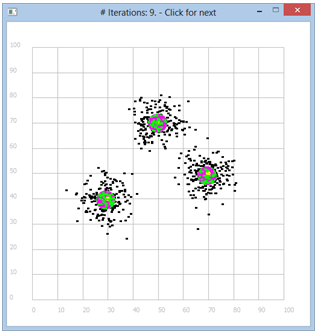
Grundprinzip des Clustering in 2 Dimensionen
 

Ein besonders einfaches Verfahren, um Cluster zu finden, ist Folgendes:

Für die Objekte muss ein Mass für den gegenseitigen Abstand definiert sein, z.B. für Punkte der Ebene (oder des Raumes) der euklidische Abstand. Ein Cluster fast einen Teil der Objektpunkte in einer Menge zusammen. Zu einer solchen Menge gehört ein Clusterzentroid, d.h. der sich wie der Schwerpunkt (Massenmittelpunkt) der Objekte (mit identischer Masse) berechnen lässt.

Zu Beginn legt man eine bestimmte Zahl von Clustern a, b, c,... mit ihren Zentroiden A, B, C, ... fest. Dann führt man iterativ aus:

Bestimme für jedes Objekt die Distanz zu den Zentroiden. Ordne den Punkt demjenigen Cluster zu, dessen Distanz am kleinsten ist. Bestimme erneute die Clusterzentroide.

(Falls zwei kleinste Distanzen gleich sind, so wähle eine davon beliebig.)

Zu Testzwecken wählen wir normalverteilte Punktwolken.

Programm: [►]

# Cluster1.py

from gpanel import *
import random
import math

# 3 clusters with id: 0, 1, 2 
# Samples: [x, y, id]

N = 200 # number per cluster
spread = 5  # cluster spread

def euklidian(pt1, pt2):
    return math.sqrt((pt1[0] - pt2[0]) * (pt1[0] - pt2[0]) + \
                     (pt1[1] - pt2[1]) * (pt1[1] - pt2[1]))

def onMousePressed(x, y):
    global nbClicks
    nbClicks += 1
    if nbClicks <= 3:
        centroid = [x, y]
        pos(centroid)
        fillCircle(4)
        centroids.append(centroid)
        if nbClicks == 3:
            title("Click to start iteration.") 
    if nbClicks > 3:
        drawCentroids()
        iterate()
        drawCentroids()
        title("# Iterations: " + str(nbClicks - 3) + ". - Click for next") 

def drawCentroids():
    for centroid in centroids:    
        pos(centroid)
        fillCircle(4)
                    
def iterate():
    # determine affiliation as shortest distance to centroid
    for pt in X:
        distances = [] # distances to centroid 0, 1, 2
        for k in range(3):
            distance = euklidian(pt, centroids[k])
            distances.append(distance)
        min_value = min(distances)    
        min_index = distances.index(min_value)
        pt[2] = min_index  # set the cluster id
    
    # determine new centroids
    xSums = [0, 0, 0]
    ySums = [0, 0, 0]
    nSums = [0, 0, 0]
    for pt in X: # each sample
        for k in range(3):  # each old centroid index
            if pt[2] == k:  # sample belongs to centroid k
                xSums[k] += pt[0]  # add x coordinate
                ySums[k] += pt[1]  # add y coordinate 
                nSums[k] += 1

    for k in range(3):        
        centroids[k][0] = xSums[k] / nSums[k] # mean of x      
        centroids[k][1] = ySums[k] / nSums[k] # mean of y      
        
makeGPanel(-10, 110, -10, 110, mousePressed = onMousePressed)
drawGrid(0, 100, 0, 100, "gray")
X = [0] * 3 * N
centroids = []
nbClicks = 0

z = [[30, 40], [50, 70], [70, 50]]
setColor("red")
for pt in z:
    pos(pt)
    fillCircle(1)
setColor("black")
    
for k in range(3):
    for i in range(N):
        rx = random.gauss(0, spread)
        ry = random.gauss(0, spread)
        x = rx + z[k][0]
        y = ry + z[k][1]
        pos(x, y)
        fillCircle(0.5)
        X[N * k + i] = [x, y, -1]
setColor("green")
setXORMode("white")
title("Click To Set 3 Centroids")
keep()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

cluster1

Bemerkungen:
Mit der Konstanten spread kann man bestimmen, wie kompakt die Clusters sind. Es ist erstaunlich, dass selbst bei weit gestreuten Clustern (z.B. spread = 10), die Clusterzentroide mit diesem einfachen Algorithmus noch gefunden werden.

 

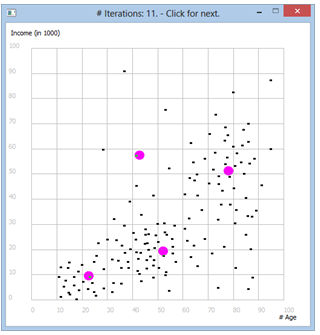
Clusteranalyse mit einer Umfrage über Einkommen und Alter
 

Nun gehen wir von einer Datensammlung aus, welche aus einer Umfrage nach Alter und Jahreseinkommen in einer bestimmten Population erfasst wurde. Wir nehmen an, dass sich drei verschiede Altersgruppen unterscheiden lassen. (Die Datensammlung samples.dat kann von hier heruntergeladen werden.)

Programm: [►]

# Cluster2.py

from gpanel import *
import math

# 3 clusters with id: 0, 1, 2 
# Samples: [x, y, id]

datafile = "samples.dat"

def euklidian(pt1, pt2):
    return math.sqrt((pt1[0] - pt2[0]) * (pt1[0] - pt2[0]) + \
                     (pt1[1] - pt2[1]) * (pt1[1] - pt2[1]))
                     
def loadData(fileName):
    try:    
        fData = open(fileName, 'r')
    except:
        return []
    out = []
    for line in fData:
        line = line[:-1]  # remove \n
        if len(line) == 0:  # empty line
            continue
        li = [i for i in line.split(",")]
        out.append(li)
    fData.close()
    return out

def onMousePressed(x, y):
    global nbClicks
    nbClicks += 1
    if nbClicks <= 3:
        centroid = [x, y]
        pos(centroid)
        fillCircle(2)
        centroids.append(centroid)
        if nbClicks == 3:
            title("Left click to start iteration.") 
    if nbClicks > 3:
        drawCentroids()
        iterate()
        drawCentroids()
        title("# Iterations: " + str(nbClicks - 3) + ". - Click for next.") 

def drawCentroids():
    for centroid in centroids:    
        pos(centroid)
        fillCircle(2)
                    
def iterate():
    # determine affiliation as shortest distance to centroid
    for pt in X:
        distances = [] # distances to centroid 0, 1, 2
        for k in range(3):
            distance = euklidian(pt, centroids[k])
            distances.append(distance)
        min_value = min(distances)    
        min_index = distances.index(min_value)
        pt[2] = min_index  # set the cluster id
    
    # determine new centroids
    xSums = [0, 0, 0]
    ySums = [0, 0, 0]
    nSums = [0, 0, 0]
    for pt in X: # each sample
        for k in range(3):  # each old centroid index
            if pt[2] == k:  # sample belongs to centroid k
                xSums[k] += pt[0]  # add x coordinate
                ySums[k] += pt[1]  # add y coordinate 
                nSums[k] += 1
    for k in range(3):        
        centroids[k][0] = xSums[k] / nSums[k] # mean of x      
        centroids[k][1] = ySums[k] / nSums[k] # mean of y      
        
makeGPanel(-10, 110, -10, 110, mousePressed = onMousePressed)
drawGrid(0, 100, 0, 100, "gray")
text(98, -8, "Age",)
text(-8, 105, "Income (in 1000)",)
data = loadData(datafile)
X = []
centroids = []
nbClicks = 0
for sample in data:
    # pt = [x-coord, y-coord, cluster_id]
    # initialize cluster_id to -1
    pt = [float(sample[0]), float(sample[1]), -1]
    X.append(pt)
    pos(pt)
    fillCircle(0.5)
setColor("green")
setXORMode("white")
title("Click to set 3 centroids")
keep()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

cluster2

Bemerkungen:
Es lassen sich 4 Einkommensgruppen von jungen Personen mit tiefem Einkommen, mittelaltrigen mit mittlerem und extrem hohem Einkommen und alte mit hohem Einkommen unterscheiden. Allerdings hängen die ermittelten Clusterzentren von der Wahl der Initialisierungspunkten ab.

 

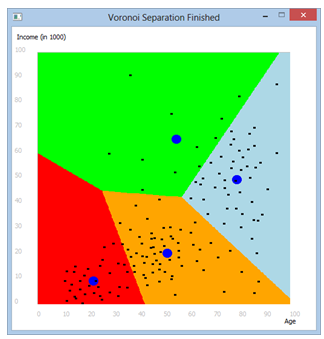
Grafische Darstellung der Zugehörigkeitsgebiete (Voronoi-Diagramm)
 

Eine gute Übersicht über die Zugehörigkeit neuer Instanzen erhält man, wenn man jeden Punkt der Ebene seinem nächstliegenden Clusterzentroid zuordnet und in unterschiedlicher Farbe färbt. Die entstehende Grafik nennt man ein Voronoi-Diagramm.

Um dieses zu zeichnen, durchläuft man alle Punkte eines engliegenden x-y-Gitters und setzt einen Farbpunkt.

Programm: [►]

# Cluster3.py

from gpanel import *
import math
import time
import thread

datafile = "samples.dat"
colors= ["red", "orange", "green", "lightblue"]
nbClusters = 4

def euklidian(pt1, pt2):
    return math.sqrt((pt1[0] - pt2[0]) * (pt1[0] - pt2[0]) + \
                     (pt1[1] - pt2[1]) * (pt1[1] - pt2[1]))

def loadData(fileName):
    try:
        fData = open(fileName, 'r')
    except:
        return []
    out = []
    for line in fData:
        line = line[:-1]  # remove \n
        if len(line) == 0:  # empty line
            continue
        li = [i for i in line.split(",")]
        out.append(li)
    fData.close()
    return out

def onMousePressed(x, y):
    global nbClicks, doPaint
    if isLeftMouseButton():
        nbClicks += 1
        if nbClicks <= nbClusters:
            centroid = [x, y]
            pos(centroid)
            fillCircle(2)
            centroids.append(centroid)
            if nbClicks == nbClusters:
                title("Left click to start iteration.")
        if nbClicks > nbClusters:
            drawCentroids()
            iterate()
            drawCentroids()
            title("# Iterations: " + str(nbClicks - 3) +
     ". - Left click for next. Right click for Voronoi separation.")
    if isRightMouseButton()and nbClicks >= nbClusters:
        thread.start_new_thread(drawVoronoi, ())

def drawCentroids():
    for centroid in centroids:
        pos(centroid)
        fillCircle(2)

def drawData():
    for sample in data:
        pt = [float(sample[0]), float(sample[1]), -1]
        X.append(pt)
        pos(pt)
        fillCircle(0.5)

def iterate():
    for pt in X:
        distances = []
        for k in range(nbClusters):
            distance = euklidian(pt, centroids[k])
            distances.append(distance)
        min_value = min(distances)
        min_index = distances.index(min_value)
        pt[2] = min_index

    xSums = [0] * nbClusters
    ySums = [0] * nbClusters
    nSums = [0] * nbClusters
    for pt in X: # each sample
        for k in range(nbClusters):
            if pt[2] == k:
                xSums[k] += pt[0]
                ySums[k] += pt[1]
                nSums[k] += 1
    for k in range(nbClusters):
        centroids[k][0] = xSums[k] / nSums[k]
        centroids[k][1] = ySums[k] / nSums[k]

def drawVoronoi():
    title("Performing Voronoi Separation...")
    step = 0.2
    setPaintMode()
    enableRepaint(False)
    pt = [0, 0]
    while pt[1] <= 100: # outer loop y direction
        while pt[0] <= 100: # inner loop in x direction
            pt[0] += step
            distances = [0] * nbClusters
            for k in range(nbClusters):
                distances[k] = euklidian(centroids[k], pt)
            min_value = min(distances)
            min_index = distances.index(min_value)
            setColor(colors[min_index])
            point(pt)
        setColor("blue")
        drawCentroids()
        repaint()
        pt[0] = 0
        pt[1] += step
    setColor("black")
    drawData()
    repaint()
    title("Voronoi Separation Finished")

makeGPanel(-10, 110, -10, 110, mousePressed = onMousePressed)
drawGrid(0, 100, 0, 100, "gray")
text(98, -8, "Age",)
text(-8, 105, "Income (in 1000)",)
setColor("black")
data = loadData(datafile)
X = []
centroids = []
nbClicks = 0
drawData()
setColor("green")
setXORMode("white")
title("Left click to set 3 centroids.")
keep()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

cluster3

Bemerkungen:
Das Zeichnen des Diagramms mit drawVoronoi() erfolgt in einem eigenen Thread, da man grundsätzlich keinen langdauernder Code in einem GUI-Callback ausführen sollte, weil während dieser Zeit das GUI eingefroren ist.

Das Voronoi-Diagramm kann mit viel effizienteren Algorithmen erstellt werden. Es handelt sich um ein klassisches Problem der Computergeometrie. Eine anschauliche Anwendung besteht darin, das Gebiet einer Stadt so einzuteilen, dass die Distanzen zu vorgegebenen Standorten von Ambulanzfahrzeugen minimal sind.

 

Interaktive Erstellung der Datensammlung
 

Zum Schluss schreiben wir noch ein kleines Programm, mit dem sich die Datensammlung durch Klicken mit der Maus interaktiv erstellen oder ergänzen lässt. Damit kann man die Clusteranalyse an eigenen Beispielen austesten.

Programm: [►]

# GenerateCluster.py

from gpanel import *

datafile = "customer.dat"

def loadData(fileName):
    try:
        fData = open(fileName, 'r')
    except:
        return []
    out = []
    for line in fData:
        line = line[:-1]  # remove \n
        if len(line) == 0:  # empty line
            continue
        li = [i for i in line.split(",")]
        out.append(li)
    fData.close()
    return out

def onMousePressed(x, y):
    global addedSamples, nbSamples
    if fOut.closed:
        return
    if isLeftMouseButton():
        pos(x, y)
        fillCircle(0.5)
        fOut.write(str(x) + "," + str(y) + "\n")
        addedSamples += 1
        title("Sample # " + str(addedSamples) + " added")
    if isRightMouseButton():
        fOut.close()
        nbSamples += addedSamples
        title("Data file closed with " + str(nbSamples) + " samples")

makeGPanel(-10, 110, -10, 110, mousePressed = onMousePressed)
drawGrid(0, 100, 0, 100, "gray")
text(98, -8, "Age",)
text(-8, 105, "Income (in 1000)",)
data = loadData(datafile)
fOut = open(datafile, "a")
setColor("black")
for sample in data:
    pt = [float(sample[0]), float(sample[1]), -1]
    pos(pt)
    fillCircle(0.5)
nbSamples = len(data)
addedSamples = 0
title(str(nbSamples) + " samples loaded")
setColor("blue")
keep()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)