Koordinatengitter

Für die Darstellung der Funktionsgrafen stehen im Modul gpanel einige praktische Werkzeuge zur Verfügung. Das Koordinatensystem kann beim Erzeugen des Grafikfensters mit makeGPanel() frei gewählt werden. Das Koordinatengitter kann mit der Funktion drawGrid() erstellt werden. Diese zeichnet für den definierten Bereich beschriftete Achsen und die passenden Gitterlinien in der gewählten Farbe. Für die fortlaufende Berechnung der Funktionswerte wird in der Regel die while-Schleife verwendet, da man in Python in einer for-Schleife nur ganzzahlige Werte für die Wertänderung verwenden kann.

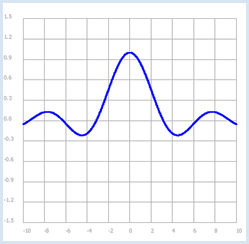
Programm: [►]

# FunctionEx1.py

from gpanel import *
from math import sin

def f(x):
    if x == 0:
        y = 1
    else:	
        y = sin(x) / x
    return y
	
makeGPanel(-12, 11, -1.8, 1.8)
drawGrid(-10, 10, -1.5, 1.5, "gray")

setColor("blue")
lineWidth(2)
x  = -10
while x < 10:
    y = f(x)
    pos(x, y) if x == -10 else draw(x, y)
    x = x + 0.01   
keep()    

Die ersten vier Parameter in der Funktion drawGrid() legen den Bereich auf der x- und y-Achse fest. In der Regel wählt man beim makeGPanel() den Koordinatenbereich ca. um 10% grösser als der Gitterlinienbereich. Es gibt mehrere überladene Version von drawGrid(). Je nachdem ob die Ticks als Integer or Float angegeben werden, werden sie auch so ausgeschrieben.

Die Funktion pos(x, y) setzt den Grafikcursor an den ersten Funktionswert. Für die Darstellung der übrigen Werte wird die Funktion draw(x, y) verwendet. Diese zeichnet jeweils eine Verbindungslinie zum nächsten Punkt. Der Grafikcursor befindet sich danach an der neuen Position.

Um die Division durch 0 bei der Berechnung der Werte sin(x)/x zu vermeiden, wird für x = 0 der Wert y = 1 gesetzt. Dieser entspricht dem Grenzwert von sin(x)/x für x → 0.

pos(x, y) if x == 10.0 else draw(x,y): Beim ersten Punkt muss der Grafikcursor mit pos() gesetzt werden, da er sich standardmässig bei (0, 0) befindet. (draw() würde den ersten Punkt mit (0, 0) verbinden.) Statt mit einem if...else-Block, kann man dies mit einer speziellen Python-Syntax erreichen, wo if und else als Teil der Anweisung verwendet wird.

Unstetige Funktionen

Die Funktion y = 2/x hat an der Selle x = 0 eine Unstetigkeitsstelle. Es gibt mehrere Möglichkeiten, bei der grafischen Darstellung mit dieser Unstetigkeitsstelle umzugehen. Am einfachsten ist, die Funktion stückweise in den stetigen Bereichen zu zeichnen.

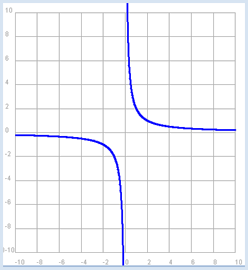
Programm: [►]

# FunctionEx2.py

from gpanel import *

def f(x):    
    y = 2 / x     
    return y
   
makeGPanel(-12, 12, -11, 11)
drawGrid(-10, 10, -10, 10, "gray")
setColor("blue")
lineWidth(2)
dx = 0.1

x  = -10.0
while x < -0.1:
    y = f(x)
    pos(x, y) if x == -10.0 else draw(x, y)
    x = x + dx 

x = 0.1
while x < 10:
    y = f(x)
    pos(x, y) if x == 0.1 else draw(x, y)
    x = x + dx     
keep() 

pos(x, y) if x == 10.0 else draw(x,y): Bei Floats (Doubles) sollte man eigentlich nie auf einen exakten Wert testen. Ausnahme: wenn man den Wert selbst setzt, wie hier x = -10.0

Exponentialfunktion

Die aus der Physik bekannte Funktion stellt eine gedämpfte harmonische Schwingung dar. Die Funktionswerte werden mit Hilfe von Funktionen exp() und sin() aus dem Modul math berechnet. Die Dokumentation zum Modul math findet man im Internet, z. B. unter https://docs.python.org/2/library/math.html

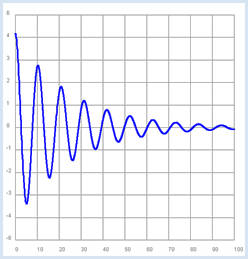
Programm: [►]

# FunctionEx3.py

from gpanel import *
from math import exp, sin, pi

def f(x):
    y = a * exp(-k * x) * sin(omega * x + fi) 
    return y
   
makeGPanel(-10, 110, -7, 7)
drawGrid(0, 100, -6, 6, "gray")

setColor("blue")
lineWidth(2)
x  = 0
a = 5
k = 0.04
omega = 0.6
fi = pi/2
dx = 0.1
while x < 100:
    y = f(x)
    pos(x, y) if x == 0 else draw(x, y)
    x = x + dx 
keep() 

from math import exp, sin, pi: Falls man die Funktionen beim import exlizit angibt,  können exp(), sin() und pi können direkt (ohne vorangestelltem math.) verwendet werden.

Funktionen in Parameterform

Die Kardiode kann in Parameterform mit folgenden Gleichung definiert werden: x = a cos φ (1 + cos φ) y = a sin φ (1 + cos φ) für 0 <= φ <= 2π.

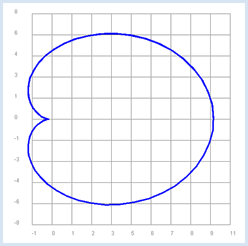
Programm: [►]

# FunctionEx4.py

from gpanel import *
from math import sin, cos, pi

def cardiode(fi):
    x = a * cos(fi) * (1 + cos(fi))
    y = a * sin(fi) * (1 + cos(fi))
    return x, y

makeGPanel(-3, 13, -10, 10)
drawGrid(-1, 11, -8, 8, "gray")

setColor("blue")
lineWidth(2)
a = 5
fi = 0
dfi = 0.1
x = 0
while fi < 2 * pi + dfi:
    x, y = cardiode(fi)
    pos(x, y) if fi == 0 else draw(x, y)
    fi = fi + dfi    
keep() 

Die Funktion cardiode() kann die beiden Werte x und y zurückgeben