Python exemplarisch
deutsch     english

FRAKTALE



 

Farn-Fraktal
   
 

Fraktale sind computergenerierte Bilder, die eine Selbstähnlichkeit aufweisen, d.h. bei denen Teilbilder ungefähr eine verkleinerte Kopie des Gesamtbildes sind. Die Algorithmen findet man in der Spezialliteratur und im Internet.

Das Farn gehört zu den bekanntesten Fraktalen. Zur Berechnung der Bildpunkte verwendet man am einfachsten komplexe Zahlen.		  

Programm: [►]

# Fern.py

from gpanel import *
import random

def fern():
    z = 0
    n = 0
    while n < nbPoints:
        r = random.random()
        c = "black"
        if r < 0.01:
            c = "yellow"
            z = f(z, 0, 0, 0, 0.16, 0, 0) # Stem
        elif r < 0.86:
            c = "green"
            z = f(z, 0.85, 0.04, -0.04, 0.85, 0, 1.60) # symmetry
        elif r > 0.86 and r < 0.93:
            c = "red"
            z = f(z, 0.20, -0.26, 0.23, 0.22, 0, 1.60)  # left leaves
        elif r > 0.93:
            c = "blue"
            z = f(z, -0.15, 0.28, 0.26, 0.24, 0, 1.44) # right leaves
        setColor(c)
        point(z)
        n += 1
        if n % 100 == 0:
			repaint()

def f(z, a, b, c, d, e, f):
    re = a * z.real + b * z.imag + e
    im = c * z.real + d * z.imag + f
    return complex(re, im)

makeGPanel(-3.5, 3.5, 0, 10)
enableRepaint(False)
bgColor("black")
nbPoints = 40000
fern()
keep()
Progammcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

  ► Erklärungen zum Programmcode
 

Bei langsamen Rechnern empfiehlt sich, die Anzahl der Punkte zu reduzieren. Eine Beschleunigung erhält man auch, indem man mit enableRepaint(False) das automatische Rendern ausschaltet und nur alle 1000 Punkte die Grafik mit repaint() rendert

 

 

Julia - Menge
 

Zur Darstellung einer Julia-Menge iteriert man die Punkte z der komplexen Ebene nach der Vorschrift

z = z2 + c

wo c eine komplexe Konstante ist. Man untersucht dabei, wie schnell der Betrag von z wächst, indem man sich einen maximalen Wert maxNorm vorgibt und die Iteration abbricht, sobald dieser Betrag überschritten wird. Je nach der Anzahl der dazu nötigen Iterationen zeichnet man den betrachteten Punkt der komplexen Ebene mit einer entsprechenden Farbe.

 

Programm: [►]

# Julia.py

from gpanel import *

def putPixel(z, c):
  setColor(c)
  point(z.real, z.imag)


maxIter = 100
maxNorm = 50.0
step = 0.005
range = 2.0
makeGPanel(-range, range, -range, range)
c = complex(-0.5, -0.5)
z0 = complex(-range, -range)
enableRepaint(False)
while z0.imag < range: # outer loop in imag direction
    z0 = complex(-range, z0.imag + step)
    while z0.real < range: # inner loop in real direction
        z0 = z0 + step
        z = z0;
        it = 0
        while (z.real * z.real + z.imag * z.imag) < maxNorm and it < maxIter:
            z = z * z + c
            it = it + 1
        if it < 3:
            putPixel(z0, "darkblue")
        elif it < 5:
            putPixel(z0, "green")
        elif it < 8:
            putPixel(z0, "red")
        elif it < 12:
            putPixel(z0, "blue")
        elif it < 100:
             putPixel(z0, "yellow")
        else:
            putPixel(z0, "black")
    repaint()   
keep()
Progammcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

  ► Erklärungen zum Programmcode
 

Wenn das Fraktal Punkt für Punkt gerendert wird, erscheint das Bild sehr langsam. Es ist daher angebracht, das automatische Rendern mit enableRepaint(False) zu deaktivieren und am Ende der inneren while-Schleife repaint() aufzurufen. Dann wird das Bild "zeilenweise" aufgebaut.

 

 

Mandelbrot-Fraktal
 
Als Vater der Fraktalen Geometrie gilt der Mathematiker Benoit Mandelbrot (1924-2010). Das nach ihm benannte Fraktal folgt dem gleichen Bildungsgesetzt wie die Julia-Menge.
  

Programm: [►]

#Mandelbrot.py

from gpanel import *

def getIterationColor(it):
    color = makeColor((30 * it) % 256, 
                      (4 * it) % 256, 
                      (255 - (30 * it)) % 256)
    return color
    
def mandelbrot(c):
    z = 0
    for it in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return it
    return maxIterations

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.003
ymin = -1.5
ymax = 1.5
ystep = 0.003

makeGPanel(xmin, xmax, ymin, ymax)
title("Mandelbrot set")
enableRepaint(False)
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        itCount = mandelbrot(c)
        if itCount == maxIterations: # inside Mandelbrot set
            setColor("yellow")
        else: # outside Mandelbrot set
           setColor(getIterationColor(itCount))
        point(c)
        x += xstep
    y += ystep
    repaint()
keep()
Progammcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

Mandelbrot mit Ausschnittsvergrösserung (Zoom)
 

Eine gute Interaktivität ergibt sich, wenn der Benutzer durch Drücken und Ziehen mit der Maus einen Ausschnitt auswählen kann, der nachfolgend wieder dargestellt wird.
Dabei kommt die Technik der Gummibandlinien zur Anwendung, wobei das Auswahlrechteck im XOR-Modus gezeichnet wird, damit es durch erneutes Zeichnen gelöscht werden kann, ohne das ganze Bild neu aufzubauen. Es ergibt sich zwar eine Verfärbung des Auswahlrechtecks, die aber in diesem Fall meist nicht als störend empfunden wird.

Programm: [►]

# Mandelbrot2.py

from gpanel import *
import thread

def getIterationColor(it):
    return (30 * it) % 256, (4 * it) % 256, (255 - (30 * it)) % 256

def mandelbrot(c):
    z = 0
    for it in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return it
    return maxIterations

def drawFractal(xmin, xmax, ymin, ymax):
    global enableZoom
    title("Mandelbrot Set. Drawing...please wait.")
    enableZoom = False
    xstep = (xmax - xmin) / 1000.0
    ystep = (ymax - ymin) / 1000.0
    clear()
    window(xmin, xmax, ymin, ymax)
    y = ymin
    while y <= ymax:
        x = xmin
        while x <= xmax:
            try:
                c = x + y*1j
                itCount = mandelbrot(c)
                if itCount == maxIterations: # inside Mandelbrot set
                    setColor("yellow")
                else: # outside Mandelbrot set
                   r, g, b = getIterationColor(itCount)
                   setColor(r, g, b)
                point(c)
                x += xstep
            except:  # Frame disposed
                return 
        y += ystep
        repaint()
    enableZoom = True
    title("Mandelbrot Set. Ready for Zooming.")

def onMousePressed(x,y):
    global x1, y1, x2, y2
    if not enableZoom:
        return
    setColor("white")
    lineWidth(3)
    setXORMode("blue") # set XOR paint mode
    x1 = x2 = x
    y1 = y2 = y

def onMouseDragged(x, y):
    global x2, y2
    if not enableZoom:
        return
    rectangle(x1, y1, x2, y2) # erase old
    x2 = x
    y2 = y
    rectangle(x1, y1, x2, y2) # draw new
    repaint()

def onMouseReleased(x, y):
    if not enableZoom:
        return
    rectangle(x1, y1, x2, y2) # erase old
    setPaintMode() # establish normal paint mode
    repaint()
    xmin = min(x1, x2)
    xmax = max(x1, x2)
    ymin = min(y1, y2)
    ymax = max(y1, y2)
    thread.start_new_thread(drawFractal, (xmin, xmax, ymin, ymax))

x1 = y1 = 0
x2 = y2 = 0
maxIterations = 50
R = 2
xmin = -2
xmax = 1
ymin = -1.5
ymax = 1.5

makeGPanel(mousePressed = onMousePressed, 
    mouseDragged = onMouseDragged, 
    mouseReleased = onMouseReleased)
title("Mandelbrot Set")
enableRepaint(False)
enableZoom = False
thread.start_new_thread(drawFractal, (xmin, xmax, ymin, ymax))
keep()

Progammcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

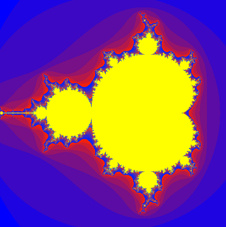
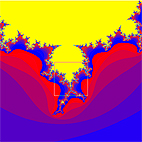
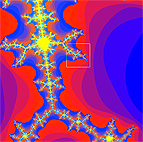
Aus der folgenden Bildsequenz ist ersichtlich, dass jede Ausschnittsvergrösserung eines Fraktals wieder ein Fraktal ist.



  ► Erklärungen zum Programmcode
 

Das Zeichnen mit drawFractal() muss in einem eigenen Thread ausgeführt werden, da Zeichnungsoperationen in Maus-Callbacks nicht sichtbar sind (auch ein repaint() nützt nichts.) Damit der Benutzer mit der Zoomoperation warten muss, bis die Zeichnung vollständig aufgebaut ist, wird das Flag enableZoom verwendet und sofort aus den Callbacks herausgesprungen, wenn es den Wert False hat.