Mustererkennung für Ziffern

 

Alle Programme können von hier heruntergeladen werden.

 

Problembeschreibung
 

Die Mustererkennung (pattern recognition) ist ein wichtiges Teilgebiet der Informatik und ist von grosser praktischen Bedeutung. Wenn es früher nur darum ging, auf Briefen die Postleitzahl zu erkennen, um die Post automatisch weiter zu leiten, wird heute die Mustererkennung beispielsweise dazu verwendet, Personen auf Grund einer Gesichtsaufnahme sogar in einer grossen Menschenmenge zu identifizieren.

Es gibt viele verschiedene Verfahren der Mustererkennung, die fast alle auch selbstlernend sind, ganz im Sinn, dass nicht nur wir, sondern auch Computer durch Fehlern klug werden.

In diesem Kapitel wenden wird den KNN-Algorithmus bei derErkennung von handgeschriebenen Ziffern an. Wir setzen voraus, dass das Kapitel "Klassifizierung (KNN)" bekannt ist.

 

Bilder als Datensätze
 
Wir gehen davon aus, dass wir schwarz-weiss Bilder der Grösse 20x20 pixel haben, auf denen in weisser Schrift eine Ziffer geschrieben ist. Die insgesamt 400 pixel haben also den Wert 0 oder 1, je nachdem, ob sie vom Schreibstift getroffen wurden oder nicht. Der Datensatz für ein Bild kann also als eine 20x20-Matrix mit 0 und 1 aufgefasst werden, in Python also als eine Liste
pic = [[0, 1, 0, 0,...][0, 0, 1, 1,...],...]
three3

Die Trainigs-Daten werden von einer einzigen Datei digits.png eingelesen, in der die handgeschriebenen Ziffern 0 bis 9 je 500 Mal gespeichert sind. Dabei befinden sich 100 Ziffernbilder in horizontaler Richtung. Für jede Ziffer werden also 5 Zeilen verwendet. Insgesamt gibt es damit in digits.png n = 5000 Ziffernbilder. (Die Datei stammt aus der Distribution von opencv und kann von hier heruntergeladen werden.)

Mit der Funktion extractPicture(img, n) wird ein einzelnes Ziffernbild n = 0..4999 aus der eingelesenen Bilddatei extrahiert, indem der Farbwert jedes Pixels gelesen und dieser in einen 0-, 1-Helligkeitswert umgewandelt wird. Das Resultat wird als pic-Liste zurück gegeben.

Für den KNN-Algorithmus muss eine Distanzfunktion zwischen zwei Instanzen definiert werden. Es ist naheliegend, diese als Totalzahl Pixels zu definieren, deren Helligkeitswerte unterschiedlich sind.

(Eigentlich handelt es sich auch hier um die euklidische Distanz

patter1

ausser, dass die Wurzel nicht gezogen wird.)

Im ersten Programm wollen wir uns lediglich mit dem Laden und Darstellen von Bildern beschäftigen und 12 Ziffernpaare darstellen, sowie ihre Distanz berechnen und ausschreiben. Wir nehmen dazu 12 Bildpaare mit unterschiedlichen Ziffern und 12 Paare mit der gleichen Ziffer.

Der Code für die Bilddarstellung ist leicht unterschiedlich, je nachdem ob wir die Python-Version oder die TigerJython-Version von GPanel verwenden. Wir berücksichtigen dies mit dem Flag isTigerJython.

Programm: [►]

# Pattern1.py

from gpanel import *
import random

def euklidian(pic1, pic2):
    # pic = [[0, 1, 0,...,1],[...],...]
    count = 0
    for i in range(20):
        for k in range(20):
            count += int(pic1[i][k] != pic2[i][k])
    return count

def extractPicture(img, n):
    # n = 0..5000
    # return list with 0, 1
    pic = [[0 for i in range(20)] for k in range(20)]
    x_offset = 20 * (n % 100)
    y_offset = 20 * (n // 100)
    for x in range(20):
        for y in range(20):
            if isTigerJython:
                c = img.getPixelColor(x + x_offset, y + y_offset)
                lum = (c.getRed() + c.getGreen() + c.getBlue()) // 3
            else:
                c = GPanel.getPixelColor(img, x + x_offset, y + y_offset)
                lum = (c[0] + c[1] + c[2]) // 3
            pic[x][y] = int(lum > 127)
    return pic

def showPicture(pic, xpos, ypos):
    if isTigerJython:
        showPictureTJ(pic, xpos, ypos)
    else:
        showPicturePy(pic, xpos, ypos)

def showPicturePy(pic, xpos, ypos):
    white = QColor(255, 255, 255).rgb()
    black = QColor(0, 0, 0).rgb()
    pm = QPixmap(20, 20)
    img = pm.toImage()
    for x in range(20):
        for y in range(20):
            if pic[x][y] == 1:
                img.setPixel(x, y, white)
            else:
                img.setPixel(x, y, black)
    image(img, xpos, ypos)

def showPictureTJ(pic, xpos, ypos):
    bm = GBitmap(20, 20)
    for x in range(20):
        for y in range(20):
            if pic[x][y] == 1:
                bm.setPixelColorStr(x, y, "white")
            else:
                bm.setPixelColorStr(x, y, "black")
    image(bm, xpos, ypos)

def getDigit(n):
    return n // 500

def loadData(filename):
    img = getImage(filename)
    out = [0] * 5000
    for n in range(5000):
        out[n] = extractPicture(img, n)
    return out

makeGPanel(Size(350, 200))
window(0, 350, 0, 200)
title("Loading data...")
X = loadData("digits.png")
title("Loading data...Done.")
count1 = 0
for i in range(12):
    pic1 = X[random.randint(0, 5000)]
    pic2 = X[random.randint(0, 5000)]
    showPicture(pic1, 30 * i, 42)
    showPicture(pic2, 30 * i, 20)
    d = euklidian(pic1, pic2)
    text(30 * i, 2, str(d))
    count1 += d
count2 = 0
for i in range(12):
    digit = random.randint(0, 9)
    pic1 = X[random.randint(500 * digit, 500 * digit + 499)]
    pic2 = X[random.randint(500 * digit, 500 * digit + 499)]
    showPicture(pic1, 30 * i, 142)
    showPicture(pic2, 30 * i, 120)
    d = euklidian(pic1, pic2)
    text(30 * i, 102, str(d))
    count2 += d
text(10, 180, "diff: " + str(count1) + "   same: " + str(count2))
keep()
Programm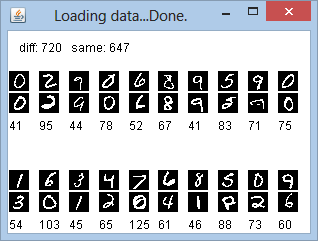code markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Resultat:
Für einen typischen Run erhält man folgende Ausgabe:

pattern2

Man erkennt, dass Paare mit gleichen Ziffern in der Regel kleinere Distanzen führen, aber nicht immer. Die Summe der Distanzen ist aber für gleiche Ziffern immer kleiner als für verschiedene Ziffern.

 

Überprüfung des Algorithmus
 

Im nächsten Schritte implementieren wir den KNN-Algorithmus und überprüfen ihn, indem wir aus den 5000 Bildern der Datensammlung 100 Bilder zufällig auswählen und als Test-Set betrachten. Die restlichen Bilder sind im Trainigs-Set.

Zur Überprüfung des Verfahrens durchlaufen wir die Instanzen des Test-Sets und schreiben aus, ob der Algorithmus die richtige oder falsche Voraussage macht.

Programm: [►]

# Pattern2.py

from gpanel import *
from operator import itemgetter
import time
import random

def euklidian(pic1, pic2):
    # pic = [[0, 1, 0,...,1],[...],...]
    count = 0
    for i in range(20):
        for k in range(20):
            count += int(pic1[i][k] != pic2[i][k])
    return count

def extractPicture(img, n):
    # n = 0..5000
    # return list with 0, 1
    pic = [[0 for i in range(20)] for k in range(20)]
    x_offset = 20 * (n % 100)
    y_offset = 20 * (n // 100)
    for x in range(20):
        for y in range(20):
            if isTigerJython:
                c = img.getPixelColor(x + x_offset, y + y_offset)
                lum = (c.getRed() + c.getGreen() + c.getBlue()) // 3
            else:
                c = GPanel.getPixelColor(img, x + x_offset, y + y_offset)
                lum = (c[0] + c[1] + c[2]) // 3
            pic[x][y] = int(lum > 127)
    return pic

def getDigit(n):
    return n // 500

def loadData(filename):
    img = getImage(filename)
    out = [0] * 5000
    for n in range(5000):
        out[n] = extractPicture(img, n)
    return out

def predict(pic0):
    distances = []
    for n in range(0, 5000):
        if n in testSample:
            continue
        pic = samples[n]
        distance = euklidian(pic0, pic)
        distances.append([n, distance])
    sorted_distances = sorted(distances, key = itemgetter(1))
    nearestPic = sorted_distances[0][0]
    return getDigit(nearestPic)

print "Loading data..."
samples = loadData("digits.png")
testSample = random.sample(range(0, 5000), 100) # 100 out of 5000
hits = 0
print "Starting test set."
for i in range(100):
    n = testSample[i]
    actual = getDigit(n)
    print "Test #", i, ": Actual digit:", actual,
    pic = samples[n]
    perceived = predict(pic)
    if perceived == actual:
        hits += 1
    print "- Perceived digit:", perceived, "-->", (perceived == actual)
print "Result: Correctly preceived", hits, "out auf 100."
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Resultat:
Für einen typischen Run erhält man folgende Ausgabe:

Loading data...
Starting test set.
Test # 0 : Actual digit: 7 - Perceived digit: 7 --> True
Test # 1 : Actual digit: 9 - Perceived digit: 7 --> False
Test # 3 : Actual digit: 7 - Perceived digit: 7 --> True
...
Result: Correctly preceived 90 out auf 100.

also eine erstaunlich gute Zuverlässigkeit der Voraussage.

 

Erkennung selbst geschriebener Ziffern
 

Schliesslich möchten wir nun tatsächlich selbst eingegebene Ziffern richtig erkennen. Dazu zeichnen wir mit der Maus in einem Feld mit der Grösse 200x200 pixel eine Ziffer, lassen diese auf 20x20 pixel schrumpfen und analysieren sie mit dem KNN-Algorithmus. Wie man zeigen kann, erhält man bereits für k = 1 eine relative gute Zuverlässigkeit. Darum vereinfachen wir den KNN-Algorithmus und betrachten nur den nächsten Nachbarn.

Um die Demonstration anschaulich zu gestalten, schreiben wird unten im Fenster noch 10 zufällig ausgewählte Ziffern des Trainings-Sets aus. Zudem erscheint rechts unten das auf 20x20 pixel verkleinerte Eingabebild, so wie es dem Analysealgorithmus übergeben wird.

Programm: [►]

# Pattern3.py

from gpanel import *
from operator import itemgetter
import time
import random

def onMousePressed(x, y):
    global isIdle, startDrawing
    if isLeftMouseButton():
        if x < -100 or x > 100 or y < -100 or y > 100:
            return
        if startDrawing:
            initGraphics()
            startDrawing = False
        pos(x, y)
    if isRightMouseButton():
        isIdle = False
        title("Working. Please wait...")
        pic = shrinkPicture()
        showPicture(pic, 160, -180)
        perceived = predict(pic)
        title("Perceived digit: " + str(perceived) + " . Draw next!")
        startDrawing = True
        isIdle = True

def onMouseDragged(x, y):
    if x < -100 or x > 100 or y < -100 or y > 100 \
        or startDrawing or not isIdle:
        return
    draw(x, y)

def euklidian(pic1, pic2):
    # pic = [[0, 1, 0,...,1],[...],...]
    count = 0
    for i in range(20):
        for k in range(20):
            count += int(pic1[i][k] != pic2[i][k])
    return count

def extractPicture(img, n):
    # n = 0..5000
    # return list with 0, 1
    pic = [[0 for i in range(20)] for k in range(20)]
    x_offset = 20 * (n % 100)
    y_offset = 20 * (n // 100)
    for x in range(20):
        for y in range(20):
            if isTigerJython:
                c = img.getPixelColor(x + x_offset, y + y_offset)
                lum = (c.getRed() + c.getGreen() + c.getBlue()) // 3
            else:
                c = GPanel.getPixelColor(img, x + x_offset, y + y_offset)
                lum = (c[0] + c[1] + c[2]) // 3
            pic[x][y] = int(lum > 127)
    return pic

def getDigit(n):
    return n // 500

def loadData(filename):
    img = getImage(filename)
    out = [0] * 5000
    for n in range(5000):
        out[n] = extractPicture(img, n)
    return out

def predict(pic0):
    distances = []
    for n in range(0, 5000):
        pic = samples[n]
        distance = euklidian(pic0, pic)
        distances.append([n, distance])
    sorted_distances = sorted(distances, key = itemgetter(1))
    nearestPic = sorted_distances[0][0]
    return getDigit(nearestPic)

def shrinkPicture():
    scaleFactor = 1 / 10.0
    if isTigerJython:
        img = getBitmap()
        cropped = GBitmap.crop(img, 100, 100, 300, 300)
        img = GBitmap.scale(cropped, scaleFactor, 0)
    else:
        img = getFullImage()
        cropped = GPanel.crop(img, 100, 100, 300, 300)
        img = GPanel.scale(cropped, scaleFactor)
    pic = toPicture(img)
    return pic

def toPicture(img):
    pic = [[0 for i in range(20)] for k in range(20)]
    for x in range(20):
        for y in range(20):
            if isTigerJython:
                c = img.getPixelColor(x, y)
                lum = (c.getRed() + c.getGreen() + c.getBlue()) // 3
            else:
                c = GPanel.getPixelColor(img, x, y)
                lum = (c[0] + c[1] + c[2]) // 3
            pic[x][y] = int(lum > 127)
    return pic

def showPicture(pic, xpos, ypos):
    if isTigerJython:
        showPictureTJ(pic, xpos, ypos)
    else:
        showPicturePy(pic, xpos, ypos)

def showPicturePy(pic, xpos, ypos):
    white = QColor(255, 255, 255).rgb()
    black = QColor(0, 0, 0).rgb()
    pm = QPixmap(20, 20)
    img = pm.toImage()
    for x in range(20):
        for y in range(20):
            if pic[x][y] == 1:
                img.setPixel(x, y, white)
            else:
                img.setPixel(x, y, black)
    image(img, xpos, ypos)

def showPictureTJ(pic, xpos, ypos):
    bm = GBitmap(20, 20)
    for x in range(20):
        for y in range(20):
            if pic[x][y] == 1:
                bm.setPixelColorStr(x, y, "white")
            else:
                bm.setPixelColorStr(x, y, "black")
    image(bm, xpos, ypos)

def initGraphics():
    lineWidth(1)
    bgColor("white")
    setColor("black")
    fillRectangle(-110, -110, 110, 110)
    text(-180, -150, "Examples:")
    setColor("white")
    lineWidth(20)
    setColor("white")
    for i in range(10):
        n = random.randint(500 * i, 500 * (i + 1) - 1)
        showPicture(samples[n], -180 + i * 22, -180)
    title("Draw a digit and click right!")

makeGPanel(Size(400, 400),
    mousePressed = onMousePressed,
    mouseDragged = onMouseDragged)
window(-200, 200, -200, 200)
title("Loading data. Please wait...")
samples = loadData("digits.png")
initGraphics()
isIdle = True
startDrawing = True
keep()

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Resultat:
Nicht alle Ziffern werden gleich gut erkannt. Für eine gute Erkennungszuverlässigkeit muss die Ziffer zudem im mittleren Bereich und mit ungefähr der gleichen Grösse wie im Trainings-Set geschrieben werden.

patterrn3

Bemerkungen:
Wir müssen auch hier für die Bildtransformationen unterscheiden, ob der Code mit TigerJython oder Python ausgeführt wird.

Es könnten noch wesentliche Verbesserungen eingebaut werden, beispielsweise eine automatische Zentrierung der Eingabe und eine Skalierung auf eine Standardgrösse.


 

Lernfähige Maschine

 

Die Zuverlässigkeit der Ziffernerkennung kann so verbessert werden, dass man das System "trainiert", d.h. an bestimmte Schreibweisen der Ziffern "gewöhnt". Dazu müsste man in einem "Lernprozess" Eingabebilder, die zu einer falschen Erkennung führen im Trainings-Set aufnehmen. Es bleibt eine durchaus lösbare Aufgabe, das entsprechende Programm zu schreiben.